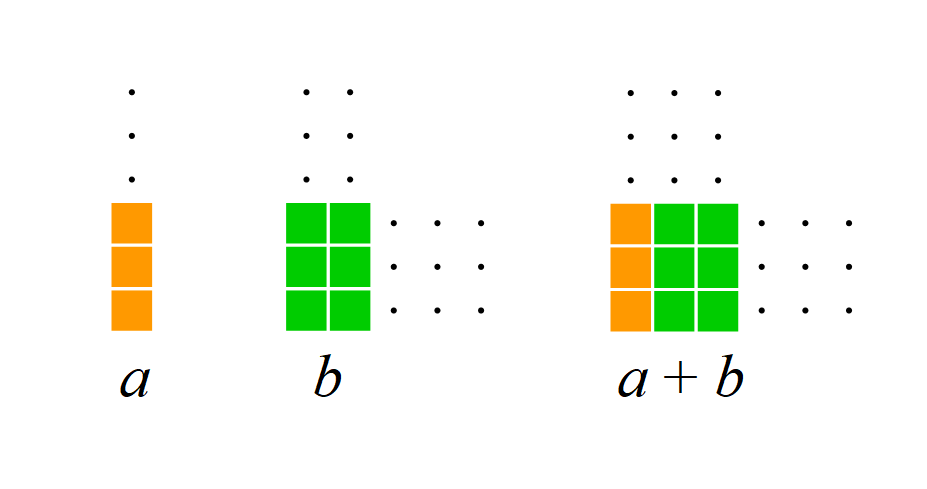Beweis des Teilbarkeitssatzes a|b und a|(b+a)

13. März 20212. April 2021 von Ferdinand Lehr

Teilt eine ganze Zahl eine andere ganze Zahl, stimmt es dann, dass die erste Zahl auch immer die Summe aus beiden Zahlen teilt? Obwohl manchen Lesern die Lösung dieses Problems instinktiv als simpel erscheinen mag, so ist die mathematisch schlüssige Begründung dazu etwas komplizierter.

Es seien $a, b$ und $n$ positive ganze Zahlen größer Null.

Behauptung:

Gilt $a \mid b$ dann gilt auch $a \mid (b+a)$

Beweis:

Wenn $a$ Teiler von $b$ ist, dann kann man $b$ schreiben als:

$b = a \cdot n$

Dies eingesetzt für $b$ in die Terme der Behauptung ergibt:

$a \mid an \mbox{~und~} a \mid (an + a) = a \mid a(n + 1)$

In beiden Ausdrücken lässt sich $a$ vollständig herauskürzen, was zeigt, dass beide Terme durch $a$ teilbar sind. (Übrig bleibt $n$ und $n+1$ )

Qed.