Das 3n+1 Problem

Im Jahr 1937 formulierte der deutsche Mathematiker Lothar Collatz eine Vermutung, die bis heute weder bewiesen noch widerlegt werden konnte. Das Problem, auch unter dem Namen Collatz-Vermutung bekannt, ist erstaunlich einfach zu beschreiben, jedoch sehr schwer zu beweisen. Nach aktuellem Forschungsstand (Februar 2021) stellt sich sogar die Frage, ob das Problem überhaupt in mathematischer Form beweisbar oder widerlegbar ist.

Die Vermutung begründet sich durch folgenden Algorithmus: Wählen Sie eine ganze Zahl größer Null. Ist die Zahl gerade, teilen Sie sie durch zwei. Ist sie ungerade, nehmen Sie sie mal drei und zählen anschließend Eins dazu. Wiederholen Sie das Halbieren oder Multiplizieren-plus-Eins solange, bis die Folge 4,2,1 dabei herauskommt.

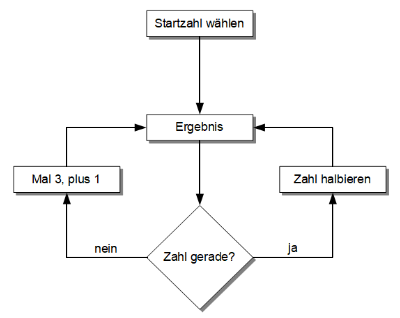
Egal welche Zahl als Startzahl gewählt wird – wenn Sie lange genug rechnen, werden Sie feststellen, dass sich am Ende immer 4,2,1 ergibt. Wirklich immer? Das fragte sich 1937 auch Lothar Collatz. Er vermutete, dass dem so sei, und seither quälen sich die Mathematiker mit diesem Problem herum, ohne dass eine beweisbare Lösung dafür gefunden werden konnte.

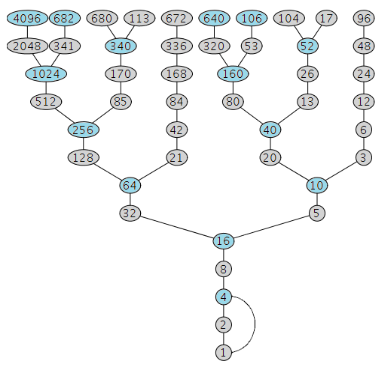
Im sogenannten Collatz-Baum sieht man den Verlauf der Rechenschritte anschaulich dargestellt. Dabei wird üblicherweise von oben nach unten gerechnet. Beispielsweise für die Startzahl 53 ergibt sich dann folgender Rechenweg:

   

Die Herausforderung liegt nun darin, zu beweisen, dass alle Startzahlen letztendlich in den Zyklus 4,2,1 münden. Wie soll das gehen? Es ist leicht einzusehen, dass man unmöglich der Reihe nach alle Zahlen einfach durchprobieren kann – das würde ewig dauern. Allerdings bekommt das Problem einen völlig neuen Aspekt, wenn man den Collatz-Algorithmus in umgekehrter Richtung betrachtet: Also mit der Zahl Eins als Startzahl und dann immer weiter mit umgedrehten Rechenbedingungen. Könnte es womöglich so einfacher sein, zu zeigen, dass alle natürlichen Zahlen sich automatisch aus dem Zyklus ergeben? Ein Ansatz dazu ist folgender:

Grundsätzlich entsteht beim umgedrehten Collatz-Algorithmus jede neue Zahl durch Verdopplung der vorhergehenden Zahl. Also z. B. 1, 2, 4, 8, … usw. Somit müssen schonmal alle Zahlen

   

in den Zyklus münden.

Nun gibt es aber spezielle Zahlen, an denen sich der Algorithmus verzweigt. Das liegt daran, dass in der ursprünglichen Form des Collatz-Algorithmus besondere Zahlen auftreten, die durch Halbierung auf dasselbe Ergebnis kommen wie jeweils eine zugehörige andere ungerade Zahl, die verdreifacht und um eins erhöht wird. Zum Beispiel:

   

   

Wir wollen diese besonderen Zahlen Verzweigungsknoten nennen. Es ist klar, dass jeder Verzweigungsknoten immer genau zwei Zweige hat; Diese Eigenschaft ergibt sich wieder aus der umgekehrten Formulierung des Collatz-Problems: Zu einem Verzweigungsknoten existieren stets zwei Nachfolger: Der eine kommt durch Verdopplung des Knotenwerts zustande, der andere durch Subtrahieren von Eins vom Knotenwert und anschließender Division durch Drei, wenn das Divisionsergebnis ungerade ist.

Die nächste Frage liegt auf der Hand: Wie oft treten denn Verzweigungsknoten auf, wenn man den positiven Zahlenstrahl (von Eins beginnend) entlanggeht? Fasst man die heute bekannten Knotenzahlen aller Zahlenfolgen, die nachweislich in den Zyklus 4,2,1 münden, als Menge zusammen, so ergibt sich:

   

Betrachtet man diese Zahlen eingehender, so scheint ab der Zahl Vier jede sechste ganze Zahl ein Verzweigungsknoten zu sein.

Behauptung:

ist immer ein Verzweigungsknoten.

Beweis:

Da durch die Collatz-Algorithmusdefinition jeder Verzweigungsknoten genau zwei Zweige besitzt, kann man argumentieren:

Für Zweig A:

kann immer verdoppelt werden.

Für Zweig B:

lässt sich schreiben als . Dieser Term enthält immer den Faktor , wegen der Teilbarkeitsgesetze und . Drittelt man außerdem so ergibt sich mit stets eine Zahl, die nicht den Faktor Zwei enthalten kann!

Somit gilt: ist immer durch Drei teilbar sowie der Ausgangswert nicht durch Zwei – womit gezeigt ist, dass ab der Zahl Vier jede sechste Zahl ein Verzweigungsknoten sein muss.

Qed.

Nun stellt sich die Frage, ob es Zahlen gibt, deren Herkunft sich nicht auf oder oder zurückführen lassen. Genau das ist der Zweifel, den auch Lothar Collatz nicht ausräumen konnte. An dieser Stelle abzubrechen wäre allerdings schade – denn bereits jetzt lassen sich interessante Schlüsse ziehen! Wir wissen nun, wie die beiden Zweige eines Verzweigungsknotens der Klasse berechnet werden:

   

   

   

Setzt man die Formel ein, so ergibt sich:

   

   

   

Gelänge es zu zeigen, dass sich mit und alle positiven natürlichen Zahlen (außer den Verzweigungsknoten) darstellen lassen, so bräuchte man lediglich noch zu beweisen, dass alle Verzweigungsknoten der Klasse in den Zyklus 4, 2, 1 oder in münden. Dies wäre sicherlich ein wichtiger Schritt auf dem Weg, die Collatz-Vermutung als richtig zu bestätigen.