Ich bin steinreich. Wer wissen will wie ich das geschafft habe, möge weiterlesen. Normalerweise entstehen Diamanten ja durch Kohlenstoffverbindungen, die durch geologische Verformungen unter der Erde unter hohem Druck, jahrtausendelang verdichtet worden sind. Industriell kann man Diamanten auch künstlich herstellen, z.B. für besonders harte Sägeblätter. Aber es gibt noch eine andere Stelle, an der die wertvollen Edelsteine auftreten: nämlich zu Hause am Computer.

Die abgebildete Grafik zeigt den Zustand einer algorithmischen Berechnungsvorschrift nach etwa einer halben Million Durchläufen. Ein einzelner Durchlauf benötigt hier ca. 0.8 Millisekunden. Das zugrundeliegende Prinzip ist ein einfacher 2D-Zellularautomat. Bei jedem Rechenschritt wird die letzte (die unterste) Zeile berechnet, und zwar immer aus der vorletzten Zeile. Danach wird das gesamte Bild nach oben verschoben, so dass die letzte Zeile frei wird, und der Vorgang beginnt von Neuem. Zu Beginn wird die unterste Zeile mit Zufallswerten gefüllt:
Startzeile = {0,0,1,1,1,1,0,1,1,1,1,1,0,1,0,0,0,0,1,1,
1,0,0,0,0,1,1,0,0,1,0,0,0,0,1,0,0,1,1,0,
0,1,1,0,1,1,1,1,1,1,1,1,1,0,1,0,1,0,0,1,
0,1,0,1,1,1,1,0,1,0,1,1,0,0,0,1,1,0,1,0,
0,0,1,0,0,0,0,1,1,0,1,0,1,1,1,1,1,1,0,1,
1,0,0,1,0,1,1,1,0,1,1,0,1,1,1,0,0,1,1,0,
1,1,0,0,1,0,1,1,1,0,1,1,1,1,0,0,1,0,1,1,
0,0,1,1,0,1,0,1,0,0,1,0,1,0,1,0,1,1,0,0}Die Folgezeilen-Berechnung ergibt sich dann aus zwei einfachen Regeln:

Für jeden neuen Bildpunkt in der letzten Zeile wird in der vorletzten Zeile nachgeguckt, wie die Bildpunkte dort gesetzt sind. Steht oben links und oben rechts eine Eins (weiß), dann ist der neue Bildpunkt ebenfalls weiß. Steht oben links und oben rechts eine Null (schwarz) und außerdem direkt darüber ebenfalls eine Null, dann wird der neue Bildpunkt schwarz. In allen anderen Fällen wird eine Null in die Folgezeile geschrieben. Bildpunkte, die außerhalb des sichtbaren Bildschirms liegen, werden außerdem als Null gewertet.
Jetzt kann die Suche losgehen. Das Bild läuft flüssig und schnell von unten nach oben und bereits jetzt sind sehr viele kleine Diamanten erkennbar. Ein Unterprogramm prüft bei jedem Durchgang, wie groß diese sind und stoppt ab einer gegebenen Mindestgröße den Programmablauf. Wie man in der Tabelle sehen kann, sind einige ziemlich große Klunker dabei herausgekommen.
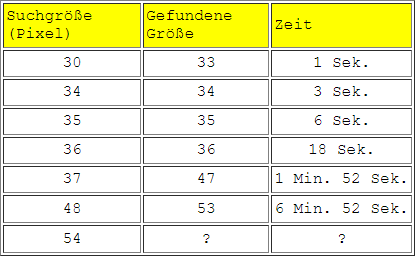
Ob es bei der gegebenen Bildbreite von 160 Bildpunkten noch größere Diamanten gibt, ist unklar. Eine mehr als zehnminütige Suche blieb ohne Ergebnis.
Quellcode (FreeBASIC):
'---------------------------------------------'
' DIAMOND-SEARCHING TOOL '
' (c) 2020 F. Lehr '
' written for FreeBASIC Compiler 1.05.0 '
'---------------------------------------------'
dim shared mx as integer = 320
dim shared my as integer = 200
dim shared amx as integer = 320/2
dim shared amy as integer = 200/2
dim shared a(mx,my) as Byte
function R1() as byte
dim r as single = rnd()
if r<0.5 then
return 0
else
return 1
end if
end function
sub drawArray()
dim as integer x,y
for y=1 to amy
for x=1 to amx
Line ( (x-1)*2, (y-1)*2 )-( (x-1)*2+1, (y-1)*2+1 ), 15*a(x,y), B
next x
next y
end sub
sub initArray()
dim as integer x,y
for y=1 to amy
for x=1 to amx
a(x,y) = 0
next x
next y
end sub
sub fillFirstLine()
'fill bottom line with random values (1 and 0)
dim as integer x
for x=1 to amx
a(x,amy) = R1()
next x
end sub
sub scrollUP()
dim as integer x,y
for y=1 to amy-1
for x=1 to amx
a(x,y) = a(x,y+1)
next x
next y
end sub
function getAbove(x as integer) as byte
if (x<1) or (x>amx) then
return 0
else
return a(x,amy-1)
end if
end function
sub calcNextLine()
'Calculate the bottom line.
dim as integer x
for x=1 to amx
if getAbove(x-1)=1 and getAbove(x+1)=1 then
a(x,amy) = 1
elseif getAbove(x-1)=0 and getAbove(x+1)=0 and getAbove(x)=0 then
a(x,amy) = 1
else
a(x,amy) = 0
end if
next x
end sub
function checkForBigTriangle(leng as integer) as integer
dim c as integer = 0
dim x as integer
for x=1 to amx
if (a(x,30)=1) then
c=c+1
if c>=leng then
'obtain real length
while x<=amx-1 and a(x+1,30)=1
x=x+1
c=c+1
wend
return c
end if
else
c=0
end if
next x
return 0
end function
'--------------------- MAIN-PROGRAM STARTS HERE ----------------------'
initArray()
fillFirstLine() 'Comment this line out, to start with zeros.
screenres mx, my
dim ctr as integer = 0
dim start as double
start = timer
dim k as string
do
k = Inkey$
screenlock()
'cls
drawArray()
screenunlock()
sleep 10
scrollUP()
calcNextLine()
ctr = ctr + 1
dim c as integer = checkForBigTriangle(35)
if c>0 then
print "" & Int(timer-start) & " sec [" & c & "] ctr=" & ctr
exit do
end if
'Save images
'if ctr>=210 and ctr<(210+200) then
'dim str1 as string = "Dia" & ctr & ".bmp"
'bsave str1, 0
'end if
If k = Chr$(27) Then
exit do
end if
loop
sleep
'--------- END OF PROGRAM ----------'