Das sogenannte „Tribar“, auch bekannt unter der Bezeichnung „Escher-Penrose-Dreieck“, kennt jeder. Obwohl diese Figur nur auf einer zweidimensionalen Fläche existieren kann, jedoch niemals im 3D-Raum, lassen sich interessante theoretische Überlegungen damit anstellen. Es ist z.B. möglich, Oberfläche und Volumen eines Tribars zu berechnen:
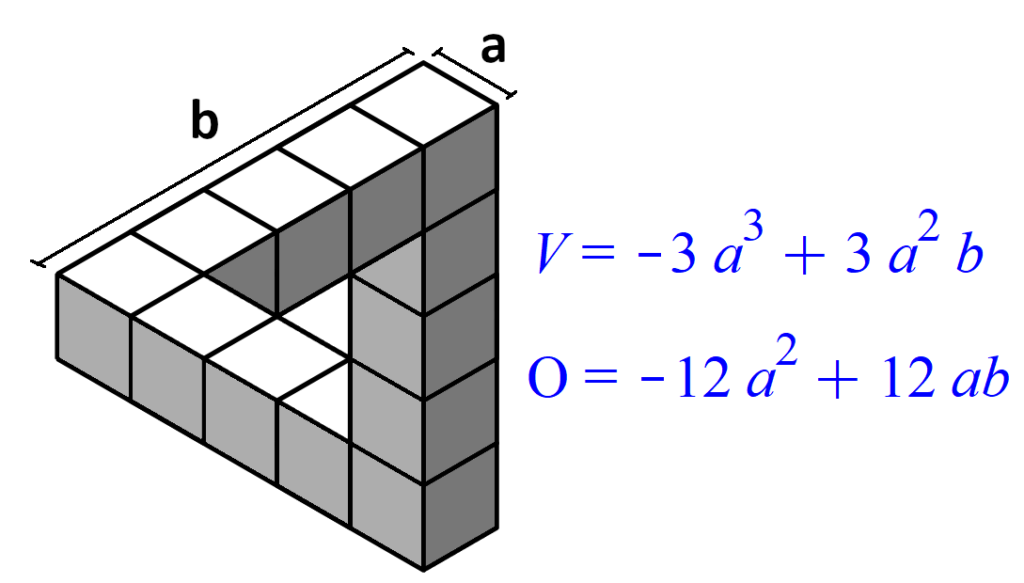
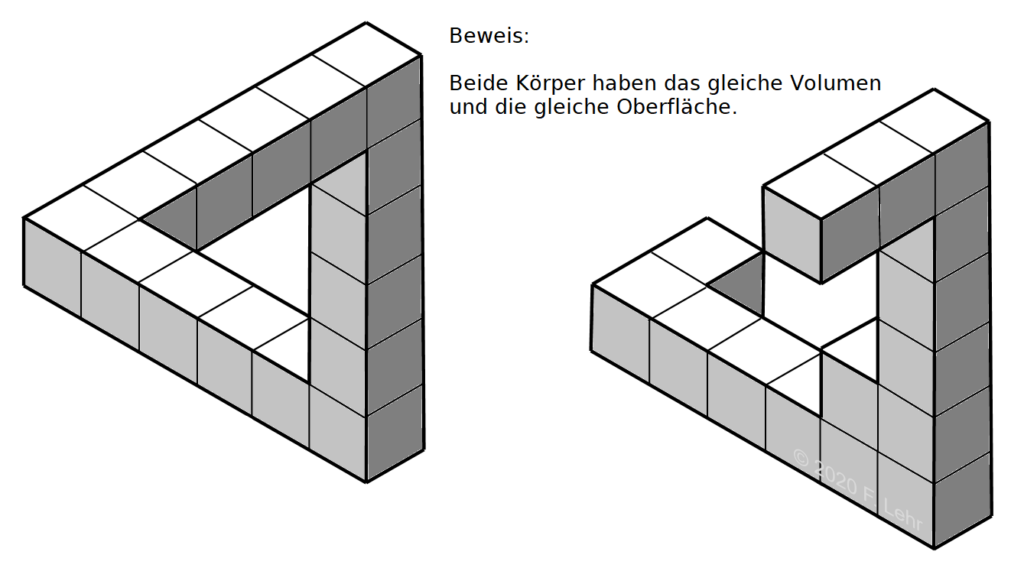
Dabei stellt sich früher oder später die Frage: Kann aus diesen beiden physikalischen Größen auf die Unkonstruierbarkeit geschlossen werden? Beim Volumen ist schnell klar, dass drei Balken mit identischen Abmessungen den entsprechenden Inhalt fassen können. Doch was ist mit der Oberfläche? Die Antwort ist: Es ist möglich, eine real baubare Figur zu konstruieren, welche bei gleichem Volumen die gleiche Oberfläche aufweist, wie das Tribar. Unterteilt man ein Tribar gleichmäßig in kleine Würfel, dann lässt sich mit einem Gedankenexperiment folgender Sachverhalt feststellen:
Ein Zwischenwürfel wird entfernt, dadurch schrumpft das Volumen des Tribars um eine Würfeleinheit, und die Oberfläche vergrößert sich um zwei Quadrateinheiten. Der entfernte Würfel behält sein Volumen, und dessen Oberfläche wächst um zwei Quadrateinheiten. Der freie Würfel wird nun in eine Ecke eingesetzt, somit wächst das Volumen des Tribars wieder um eine Würfeleinheit, und die Oberfläche verliert zwei Quadrateinheiten. Der hinzugefügte Würfel bleibt im Volumen gleich, verliert aber ebenfalls wieder zwei Quadrateinheiten.
Weitere Berechnungen
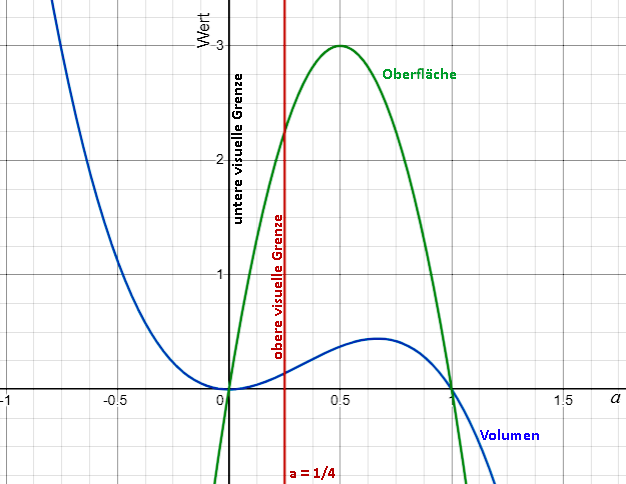
Es stellt sich heraus, dass bei fixer Balkenlänge b=1 die Oberfläche und das Volumen eines Tribar maximal die Werte 9/4 bzw. 9/64 annehmen kann, ohne dass die obere optische Grenze überschritten wird. Der Durchmesser des Lochs in der Mitte des Tribar wird dabei Null. Umgekehrt würde bei minimaler Balkendicke (a=0) der Tribar komplett verschwinden. Seine maximale Oberfläche erreicht das Tribar bei einer Balkendicke von a=1/2, das maximale Volumen bei a=2/3. Beide Werte liegen jenseits der oberen optischen Grenze; vergrößert man a weiter, so beginnen Oberfläche und Volumen wieder zu schrumpfen und werden bei a=1 schließlich beide Null.